Moving Average - Скользящее Среднее
Виды скользящей средней:
1) Simple Moving Average (SMA) - простое скользящее среднее;
2) Exponential Moving Average (EMA) - экспоненциальное скользящее среднее;
3) Smoothed Moving Average (SMMA) - сглаженное скользящее среднее;
4) Linear Weighted Moving Average (LWMA) - линейно-взвешенное скользящее среднее.
Скользящее среднее определяет среднее значение цены инструмента за определенный отрезок времени.
Виды скользящих средних отличаются друг от друга весовыми коэффициентами, присваиваемыми последним данным. В простом среднем все цены определенного периода имеют равный вес, в случае экспоненциальных и взвешенных более весомыми являются последние цены.
При расчете скользящего среднего учитываются цены открытия и закрытия, максимальная и минимальная цены, объем торгов и в некоторых случаях значения других индикаторов, а также скользящие средние самих скользящих средних.
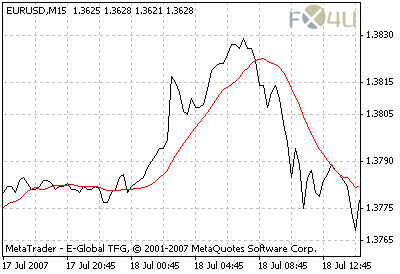
Сигналы к покупке и к продаже по Moving Average возникают, когда цена пересекает линии индикатора и идет соответственно вверх или вниз.
скользящие средние предоставляет возможность торговать по тренду, не обеспечивая при этом вхождение в рынок строго в низшей точке, а выход - на вершине.
Скользящие средние также могут применяться в сочетании с другими forex индикаторами.
Как рассчитать:
1) Простое скользящее среднее (Simple Moving Average, SMA)
Простое, или арифметическое, скользящее среднее рассчитывается путем сложения цен закрытия инструмента за определенное число единичных периодов (например, 12 часов), а получившаяся сумма затем делится на число периодов.
SMA = S (CL (i), X) / X
Где:
S - сумма;
CL (i) - цена закрытия текущего периода;
X - число периодов расчета.
2) Экспоненциальное скользящее среднее (Exponential Moving Average, EMA)
Экспоненциально сглаженное скользящее среднее определяется путем прибавления к предыдущему значению скользящего среднего определенной доли текущей цены закрытия. В случае экспоненциальных скользящих средних большую значимость представляют последние цены закрытия. Р-процентное экспоненциальное скользящее среднее будет иметь вид:
EMA = (CL (i) * P) + (EMA (i - 1) * (100 - P))
Где:
CL (i) - цена закрытия текущего периода;
EMA (i - 1) - значение скользящего среднего предыдущего периода;
P - доля использования значения цен.
3) Сглаженное скользящее среднее (Smoothed Moving Average, SMMA)
Первое значение этой сглаженной рассчитывается, как и простая скользящая средняя (SMA).
SUM1 = S (CL (i), X)
SMMA1 = S1 / X
Второе и последующие скользящие средние рассчитываются по следующей формуле:
SMMA (i) = (S1 - SMMA (i - 1) + CL (i)) / X
Где:
S - сумма;
S1 - сумма цен закрытия N периодов, отсчитываемая от предыдущего бара;
SMMA (i - 1) - сглаженное скользящее среднее предыдущего бара;
SMMA (i) - сглаженное скользящее среднее текущего бара (кроме первого);
CL (i) - текущая цена закрытия;
X - период сглаживания.
4) Линейно-взвешенное скользящее среднее (Linear Weighted Moving Average, LWMA)
При расчете взвешенного скользящего среднего последние данные имеют большее значение, чем более ранние. Взвешенное скользящее среднее вычисляется умножением каждой из цен закрытия в рассматриваемом ряду на определенный весовой коэффициент.
LWMA = S (CL (i) * i, X) / S (i, X)
Где:
S - сумма;
CL(i) - текущая цена закрытия;
S (i, X) - сумма весовых коэффициентов;
X - период сглаживания.